
- Autor Stanley Ellington ellington@answers-business.com.
- Public 2023-12-16 00:23.
- E modifikuara e fundit 2025-01-22 16:14.
Regresion i shumëfishtë analiza përdoret për të ekzaminuar lidhjen midis një ndryshoreje numerike, të quajtur kriter, dhe një grupi variablash të tjerë, të quajtur parashikues. Përveç kësaj, regresioni i shumëfishtë analiza përdoret për të hetuar korrelacionin midis dy variablave pas kontrollit të një kovariati tjetër.
Për më tepër, çfarë do të thotë regresion i shumëfishtë?
Regresion i shumëfishtë është një shtrirje e thjeshtë lineare regresioni . Përdoret kur duam të parashikojmë vlerën e një ndryshoreje bazuar në vlerën e dy ose më shumë variablave të tjerë. Ndryshorja që duam të parashikojmë quhet variabli i varur (ose ndonjëherë, variabli rezultati, objektivi ose kriteri).
Në mënyrë të ngjashme, çfarë është analiza e regresionit të shumëfishtë në kërkime? Analiza e regresionit të shumëfishtë është një teknikë e fuqishme që përdoret për parashikimin e vlerës së panjohur të një ndryshoreje nga vlera e njohur e dy ose më shumë variablave - të quajtur edhe parashikues.
Lidhur me këtë, cili është një shembull i regresionit të shumëfishtë?
Për shembull , nëse jeni duke bërë një regresioni i shumëfishtë për t'u përpjekur të parashikoni presionin e gjakut (variabli i varur) nga variabla të pavarur si gjatësia, pesha, mosha dhe orët e ushtrimit në javë, do të dëshironit gjithashtu të përfshini seksin si një nga variablat tuaj të pavarur.
Çfarë është regresioni linear në psikologji?
Regresionit linear është një formë e regresioni analiza në të cilën marrëdhënia ndërmjet një ose më shumë ndryshoreve të pavarura dhe një ndryshoreje tjetër, e quajtur variabla e varur, modelohet nga një funksion i katrorëve më të vegjël, i quajtur një regresionit linear ekuacioni. Rezultatet i nënshtrohen analizave statistikore.
Recommended:
Çfarë është vlerësimi i shumëfishtë i tregut?
Në ekonomi, vlerësimi duke përdorur shumëfish, ose "vlerësimi relativ", është një proces që konsiston në: identifikimin e aktiveve të krahasueshme (grupi i kolegëve) dhe marrjen e vlerave të tregut për këto pasuri. shndërrimi i këtyre vlerave të tregut në vlera të standardizuara në lidhje me një statistikë kryesore, pasi çmimet absolute nuk mund të krahasohen
Çfarë është regresioni linear Python?
Regresioni linear (Zbatimi i Python -it) Regresioni linear është një qasje statistikore për modelimin e marrëdhënieve midis një ndryshoreje të varur me një grup të caktuar ndryshoresh të pavarura. Shënim: Në këtë artikull, ne i referohemi variablave të varur si përgjigje dhe variablave të pavarur si veçori për thjeshtësi
Çfarë është regresioni logjistik në minierat e të dhënave?
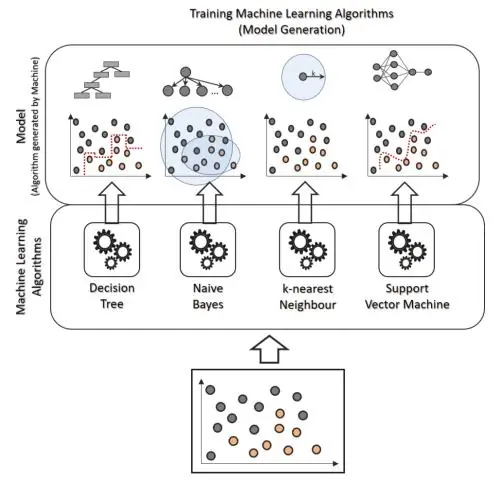
Regresioni logjistik është një metodë analize statistikore e përdorur për të parashikuar një vlerë të dhënash bazuar në vëzhgimet e mëparshme të një grupi të dhënash. Një model i regresionit logjistik parashikon një variabël të të dhënave të varur duke analizuar marrëdhënien midis një ose më shumë variablave të pavarur ekzistues
Çfarë është regresioni linear i shumëfishtë në R?
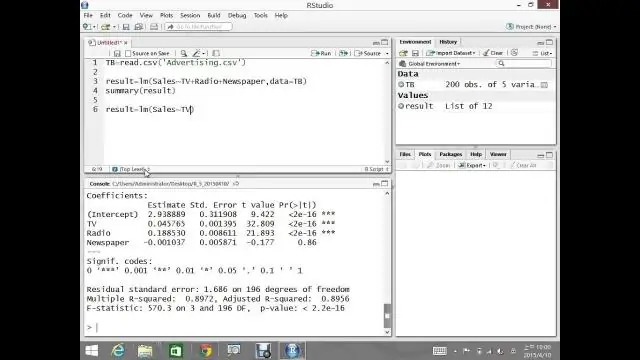
Regresioni linear i shumëfishtë është një shtrirje e regresionit të thjeshtë linear që përdoret për të parashikuar një variabël rezultati (y) në bazë të variablave të shumëfishta parashikuese të dallueshme (x). Ata matin lidhjen midis variablit parashikues dhe rezultatit
Çfarë ju thotë regresioni i shumëfishtë?

Regresioni i shumëfishtë është një shtrirje e regresionit të thjeshtë linear. Përdoret kur duam të parashikojmë vlerën e një ndryshoreje bazuar në vlerën e dy ose më shumë variablave të tjerë. Ndryshorja që duam të parashikojmë quhet variabli i varur (ose ndonjëherë, variabli rezultati, objektivi ose kriteri)
